In this blog i am going to discuss about sum of infinity series by unconventional method which gives strange result this master piece of calculating infinity series was derived by a Indian mathematician Srinivasa Ramanujan , who discovered mind blowing result .

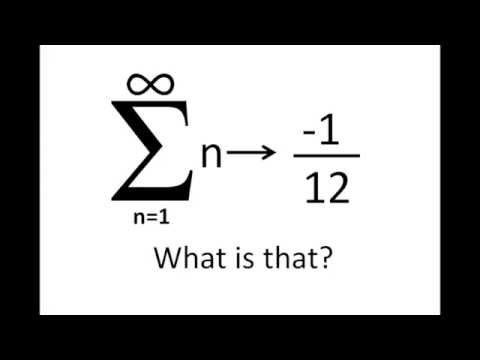
if i ask you what is the sum of all natural number , more likely you will answer  “infinity” right , but as always genius personalities has different opinion than others just like srinivasa Ramanujan .

Lets see how 

                  1+2+3+4+5+6+7+8+9 . . . . . .

Became

-1/12

Let’s take a infinite series S1 –

S1 = 1-1+1-1+1-1+1-1+1-1+1 . . . . . .

lets do little maneuver with it like we always do in mathematics – 

S1 = (1-1)+(1-1)+(1-1)+(1-1)+(1-1)+(1-1). . . . . . 

we are just taking brackets at first on “plus one” and than closing it after “negative one” and we don’t know infinite is either even term  or odd term so lets take above S1 series as even .

AGAIN – 

S1= 1(-1+1) (-1+1) (-1+1) (-1+1) (-1+1)(-1+1) . . . . . .

Don’t get confused that there is multiplication between brackets if you have doubt ask me in the comments !

Now here we are taking brackets at first on “negative one” and closing it after ‘plus one” and let this series as odd .

S1=

so result’s will be  – 

S1 = 0   (even term) 

S1 = 1 (odd term) 

Now result of same series is 0 and 1 so we will take average of it now S1 becomes 

S1 = (0+1)/2

S1 = 1/2 —-> eq(1)

Now we will take another series as S2 – 

So we are writing S2 two times and second time by sliding it one digit right & 1 of “second time written S2” will come just below the 2 of “first time written S2 series” .

sliding digits will make no difference as it is a infinite series we are talking about .

and by adding both of the series we will come on the conclusion of –

2*S2 = 1-1+1-1+1-1+1 . . . . . .

and right hand side is equal to S1 by eq (1)= 1/2

So, S2 becomes – 1/4 —–> eq(2) .

Now we have reached to our decisive part – 

so we will take here one new series as S3 

S3= 1+ 2+3+4+5+6+7+8 . . . . . .—–> eq(3) .

And we will subtract  S2 by S3 

= 0+4+0+8+0+12+0+16 . . . . . .

( S3 – S2 ) = 4+8+12+16 . . . . . . 

S3 – S2 = 4 ( 1+2+3+4+5+6+7+8+9 . . . . . .)

We can write it as by eq(2) & eq(3) as

(S3 – (1/4)) = 4*(S3)

And by transferring S3 right hand side we have – 

-1/4 = 4*S3 – S3

-1/4 = 3*S3

FINAL CONCLUSION IS – 

S3 = -1/12

you can say that this is like a mathematical trick and if you think like that than congratulation’s you unknowingly joined a group with huge number of following’s but this is true , if mathematical prediction’s goes wrong or makes any contradiction we immediately remove that concept because mathematics don’t allow any concept without proof and Ramanujan proved it , also this result are used in various theories of physics like string theory and quantum mechanics  and working with 100 % compatibility. as for as string theories concern one can’t prove a 26 dimension’s concept without this result at all .